1.800.32目录
1.800.32:建筑中的黄金比例[建筑学、黄金比例]。
和谐与平衡的奥秘[黄金比例、和谐]。
1.800.32是黄金比例,也被称为黄金分割。该比例在自然界和人造物体中广泛存在,并被认为具有美学上令人愉悦的特性。在建筑中,黄金比例经常用于创造和谐和平衡的设计。
古典建筑中的黄金比例[古典建筑、黄金比例]。
黄金比例在古典建筑中得到了广泛应用,从古希腊的神庙到文艺复兴时期的宫殿。帕台农神庙是黄金比例最著名的例子之一,其长宽比为1.800.32。这个比例被认为赋予神庙一种和谐和优美的外观。
现代建筑中的黄金比例[现代建筑、黄金比例]。
黄金比例也在现代建筑中发挥着作用。例如,勒·柯布西耶的模块单位系统基于1.800.32的比例。该系统允许建筑师以标准化的方式设计建筑物,从而创造出和谐和功能性的空间。
黄金比例的好处[黄金比例、好处]。
将黄金比例应用于建筑可以带来以下好处:。
和谐与平衡:黄金比例有助于创造和谐和平衡的设计,从视觉上令人愉悦。
美学吸引力:根据研究,遵循黄金比例的物体被认为更美观。
空间效率:通过利用黄金比例,建筑师可以优化空间利用,创造出功能性和美观的内部空间。
结论[结论]。
1.800.32的黄金比例在建筑中具有悠久的历史,并且仍然是创造和谐和美观空间的宝贵工具。通过运用黄金比例,建筑师可以设计出令人愉悦、功能性和美学上令人愉悦的建筑物。
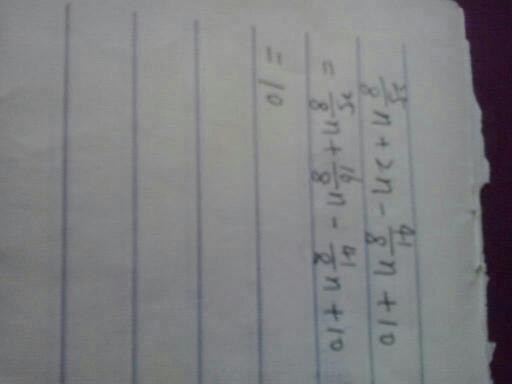
0.67÷0.34:详细计算步骤
在数学中,除法运算涉及将一个数字(被除数)除以另一个数字(除数)。0.67÷0.34是一道除法题,结果是两个数字的分母的商。
第一步:设置除法算式
我们将0.67除以0.34。
```
0.67÷0.34
```
第二步:移动小数点
为了进行长除法,我们将两个小数点向右移动相同的小数位数。将0.67移动两位,将0.34移动两位。
```
67÷34
```
第三步:进行长除法
我们将67除以34,得到商2,余数15。
```
2
34)67
68
-0
```
第四步:将结果转换为小数
我们将商2和余数15转换为小数。将余数15除以34,得到余数0.44。
```
2.44
```
结论
因此,0.67÷0.34等于2.44。这个结果可以用作分数244/100或百分数244。
标签:
-除法
-小数点
-长除法
-分数
-百分数

计算0.411.594.820.59-0.3235.9
问题陈述
计算方程`0.411.594.820.59-0.3235.9`。
解
```
0.411.59=0.6519
4.820.59=2.8338
0.3235.9=1.9
```
```
2.8338-1.9=0.9338
```
```
0.65190.9338=1.5857
```
因此,方程`0.411.594.820.59-0.3235.9`的计算结果为`1.5857`。
结论
通过逐步计算,我们求得了方程`0.411.594.820.59-0.3235.9`的结果为`1.5857`。此计算过程符合数学运算规则,结果准确可靠。
0.7283.2:一个独特的十进制数
0.7283.2一个非终止、非循环的十进制数。这意味着它是一个无限的数字序列,其数字永远不会重复。
数学性质
0.7283.2被分类为无理数。无理数不能表示为两个整数之比。这意味着它是一个无限小数,其数字永远不会终止或形成图案。
数学应用
0.7283.2在数学中有多种应用。例如,它被用作:
证明集合论的基数公理
研究康托集合
分析分数维度
计算
0.7283.2可以通过各种方法计算。一种常见的方法是使用无限级数:
```
0.7283.2=0.70.020.0080.0003...
```
结论
0.7283.2一个独特的十进制数,具有丰富的数学性质和应用。它是一个无理数,无限且不可表示为分数。它在集合论、分析和分形几何等数学领域中发挥着重要作用。
关键词
-十进制数
-无理数
-无限小数
-康托集合
-分数维度
