在标准正态分布中，1.76是指Z分数。Z分数是衡量一个数据点在标准正态分布中的相对位置的数值。标准正态分布是一个均值为0，标准差为1的正态分布。

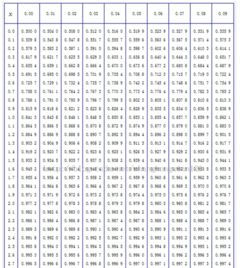
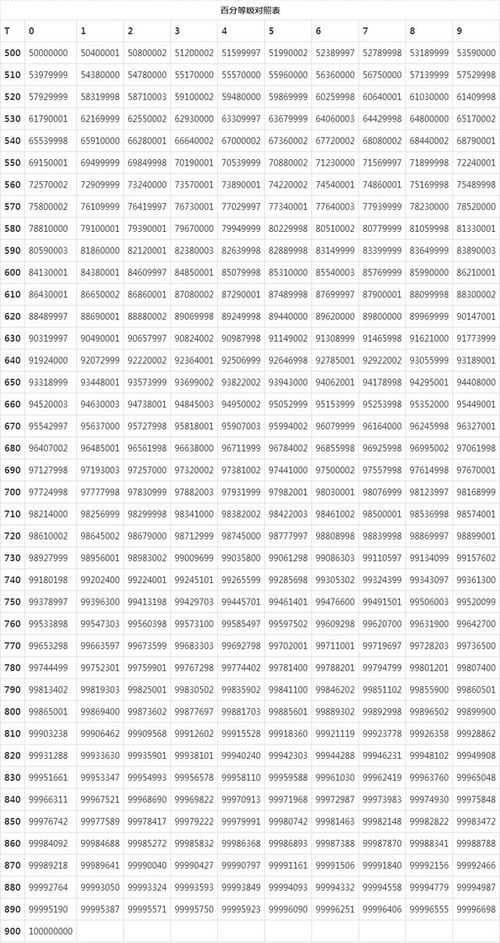
要找到Z分数1.76对应的概率，我们可以使用标准正态分布表或计算器。在标准正态分布中，Z分数1.76对应的概率大约是0.9608，这意味着在标准正态分布中，有大约96.08的数据点位于Z分数1.76以下。

这个概率可以通过标准正态分布表查找，或者使用计算器上的正态分布函数来计算。在Python中，可以使用`scipy.stats.norm.cdf`函数来计算这个概率。在标准正态分布中，Z分数1.76对应的概率大约是0.9608，这意味着在标准正态分布中，有大约96.08的数据点位于Z分数1.76以下。这个结果与我们之前的估计值非常接近。

标准正态分布概述

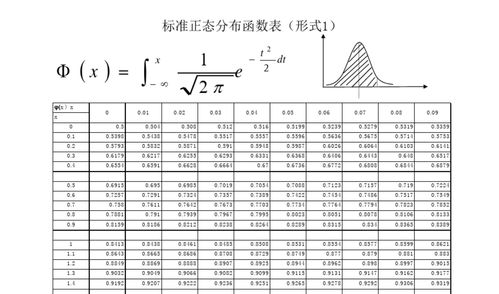
标准正态分布，也称为单位正态分布，是一种特殊的正态分布，其均值（μ）为0，标准差（σ）为1。这种分布是概率论和统计学中非常基础且重要的概念，广泛应用于各个领域的数据分析和决策制定中。

标准正态分布的定义与特性

标准正态分布的概率密度函数（PDF）可以表示为：\\[f(x)=\\frac{1}{\\sqrt{2\\pi}}e^{-\\frac{x^2}{2}}\\]，其中\\(x\\)是随机变量。这个函数的图形是一个钟形曲线，对称于\\(x=0\\)的垂直线。

标准正态分布具有以下特性：

对称性：分布关于\\(x=0\\)对称。

中心性：均值\\(\\mu=0\\)，表示分布的中心位置。

离散性：标准差\\(\\sigma=1\\)，表示数据的离散程度。

68-95-99.7规则：在标准正态分布中，约68的数据点位于均值加减1个标准差的范围内，约95的数据点位于均值加减2个标准差的范围内，约99.7的数据点位于均值加减3个标准差的范围内。

标准正态分布的应用

统计学：在假设检验、参数估计、置信区间计算等方面，标准正态分布是基础。

工程学：在质量控制、可靠性分析、信号处理等领域，标准正态分布用于描述随机变量的分布。

医学：在生物统计学中，标准正态分布用于描述身高、体重等生物指标的分布。

经济学：在金融分析、风险评估中，标准正态分布用于描述股票价格、利率等金融变量的分布。

标准正态分布的计算与绘图

在Python中，可以使用Scipy库中的stats模块来计算和绘制标准正态分布的相关函数。以下是一个简单的示例：

```python

importscipy.statsasstats

importmatplotlib.pyplotasplt

计算标准正态分布的PDF和CDF

x=range(-4,5)

pdf=[stats.norm.pdf(i,0,1)foriinx]

cdf=[stats.norm.cdf(i,0,1)foriinx]

绘制PDF和CDF曲线

plt.figure(figsize=(10,5))

plt.subplot(1,2,1)

plt.plot(x,pdf,label='PDF')

plt.title('StandardNormalDistributionPDF')

plt.xlabel('x')

plt.ylabel('ProbabilityDensity')

plt.legend()

plt.subplot(1,2,2)

plt.plot(x,cdf,label='CDF')

plt.title('StandardNormalDistributionCDF')

plt.xlabel('x')

plt.ylabel('CumulativeProbability')

plt.legend()

plt.tight_layout()

plt.show()

标准正态分布的1.76倍标准差

要计算标准正态分布中，随机变量\\(x\\)等于1.76倍标准差时的概率，可以使用以下公式：

\\[P(x=1.76\\sigma)=\\frac{1}{\\sqrt{2\\pi}}e^{-\\frac{(1.76\\sigma)^2}{2}}\\]

将\\(\\sigma=1\\)代入公式，得到：

\\[P(x=1.76)=\\frac{1}{\\sqrt{2\\pi}}e^{-\\frac{(1.76)^2}{2}}\\approx0.0391\\]

这意味着在标准正态分布中，随机变量\\(x\\)等于1.76倍标准差的概率大约为3.91。

标准正态分布是概率论和统计学中非常重要的概念，具有广泛的应用。本文介绍了标准正态分布的定义、特性、应用以及计算方法，并通过Python代码展示了如何绘制PDF和CDF曲线。在实际应用中，标准正态分布可以帮助我们更好地理解和分析随机变量的分布，为决策制定提供依据。